Sequência de Fibonacci, o que é?

Muitas pessoas já ouviram falar sobre a sequência de Fibonacci, um dos elementos matemáticos mais comuns na cultura popular, desde filmes e séries, até em aplicações práticas e em desenhos.

Esse padrão engraçado parece até mágica, mas tem um estudo sólido por trás, o que permite seu uso em várias áreas.

O que é a sequência de Fibonacci?

Via Superinteressante

A sequência de Fibonacci é uma sequência matemática infinita de números que começa com 0 e 1, e cada número subsequente na sequência é a soma dos dois números anteriores. Portanto, a sequência começa assim:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

A fórmula matemática para calcular o enésimo número na sequência de Fibonacci é a seguinte, onde n é o índice do número desejado:

F(n) = F(n-1) + F(n-2)

Por exemplo, para calcular o 7º número na sequência de Fibonacci (índice n = 7), você somaria os números F(6) e F(5), que são 8 e 5, respectivamente, resultando em 13, que é o 7º número na sequência.

Quem criou?

A sequência de Fibonacci foi introduzida ao mundo ocidental pelo matemático italiano Leonardo de Pisa, que ficou conhecido como Fibonacci. Ele viveu durante o século XIII, mais precisamente de 1170 a 1250.

Leonardo de Pisa não foi o criador da sequência, mas ele desempenhou um papel fundamental em sua popularização no Ocidente e na divulgação de suas propriedades matemáticas.

A sequência de Fibonacci já era conhecida em outras partes do mundo, como na Índia, onde era chamada de “sequência de números hindus”. No entanto, a obra de Fibonacci, chamada “Liber Abaci” (O Livro do Ábaco), publicada em 1202, trouxe essa sequência à atenção da Europa.

Em “Liber Abaci”, o autor descreveu a sequência de Fibonacci como um exemplo de como os coelhos se reproduziriam ao longo do tempo. Ele começou com um par de coelhos, imaginando que eles se reproduziriam a cada mês, e usou a sequência para representar o número de coelhos após cada mês.

Essa abordagem tornou a sequência de Fibonacci mais acessível e fácil de entender para as pessoas da época.

Desde então, essa lógica se tornou um tópico significativo na matemática e tem várias aplicações em diversas áreas do conhecimento.

Espirais áureas

Via Planeta Biologia

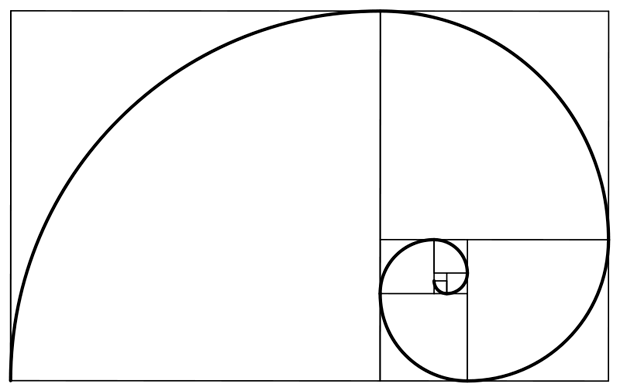
Outra aplicação famosa da sequência de Fibonacci está nas espirais matemáticas, que levam o nome de “espiral áurea”. Essa figura surge usando quadrados cujos lados têm comprimentos iguais aos números na sequência de Fibonacci.

A construção da espiral de Fibonacci é feita da seguinte maneira:

1. Comece com dois quadrados, um com lado de comprimento 1 e outro com lado de comprimento 1. Coloque-os lado a lado.
2. Em seguida, adicione um terceiro quadrado, cujo lado tem comprimento igual à soma dos lados dos dois primeiros quadrados (1 + 1 = 2). Coloque-o adjacente aos dois primeiros, formando um retângulo.
3. Continue adicionando quadrados ao retângulo, com lados de comprimentos iguais à soma dos dois quadrados anteriores.
4. Repita esse processo indefinidamente, criando uma sequência de quadrados que cresce de acordo com a sequência de Fibonacci.

À medida que você adiciona mais e mais quadrados, a espiral resultante se aproxima de uma forma geométrica chamada espiral logarítmica, com várias propriedades interessantes.

Por exemplo, a razão entre o comprimento de dois lados consecutivos na espiral de Fibonacci se aproxima da proporção áurea (Phi), que é aproximadamente igual a 1,618033988749895…

Além disso, a espiral de Fibonacci existe em muitos fenômenos naturais, como nas sementes em uma flor de girassol, nas galáxias espirais e a espiral dos chifres de carneiro.

Essa imagem também é frequentemente usada em arte e design devido à sua estética agradável e à conexão com a proporção áurea, que é considerada esteticamente agradável.

Aplicações modernas

Via NOIZE

A sequência de Fibonacci continua a ter várias aplicações modernas em diversas áreas.

Ela aparece frequentemente em algoritmos e programação, como na busca binária e análise recursiva. Com essa lógica, é possível criar vários programas, inclusive de previsões para o mercado financeiro.

Ainda, a sequência e sua espiral estão em muitos padrões da natureza, incluindo a disposição de folhas em plantas, a estrutura de cones de pinheiros e a espiral de moluscos. Esses padrões têm implicações em campos como botânica, biologia evolutiva e genética.

Enquanto isso, arquitetos e designers frequentemente fazem uso da proporção áurea, que está relacionada à sequência de Fibonacci, para criar edifícios, obras de arte e produtos esteticamente agradáveis. Modelagens 3D e design gráfico também replicam esse modelo.

Na comunicação, auxilia na codificação e correção de erros em sistemas de transmissão informática.

Ou seja, Fibonacci está em tudo, e sua sequência, embora não pareça se relacionar com a maioria dos assuntos, foi o que tornou tantas inovações possíveis.

Fonte: Mistérios do Mundo

Imagens: Planeta Biologia, NOIZE, Superinteressante